频谱泄露是频谱分析的常见问题，它来源于傅里叶变换的基本原理，当非周期的信号经过傅里叶变换后就会产生泄露的现象。

泄露的产生

傅里叶变换的公式：

s_x(f)=\int^{\infty}_{-\infty}{x(t)e^{-j2{\pi}ft}dt}

离散傅里叶变换公式：

s_x(m\delta{f})=\delta{t}\sum^{\infty}_{-\infty}{x(n{\delta}{t})e^{-j2{\pi}m{\delta}fn{\delta}t}}

但是在实际采集过程中只能采集一定范围内的数据，当采集到的信号是周期的整数倍时，通过在时域上重复这部分信号可以重现原始信号，但是如果采集到的信号不是周期的整数倍时，则无法重现原始信号。反映到频域中就是频谱泄露。

以正弦波为例，以整周期采样时得到的频谱是一条谱线，非整周期时该谱线的能量被“泄露”到旁边：

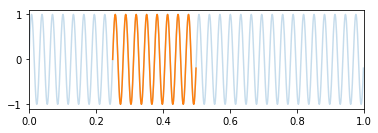
减小泄露的方法

泄露只能减少，无法消除。常见的减小泄露的方法有以下几种：

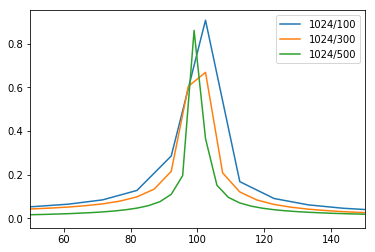
增加频域分辨率

增加频域分辨率即减小{\delta}f“, 泄露在更小的频率范围内迅速衰减。具体的方法就是减小采样率或增加采样点数。如图所示：

窗函数

窗函数是对时域信号的一种加权，使得加窗后的信号更具有周期性。如图所示：

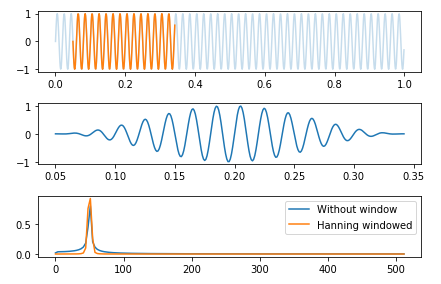
加窗可以有效减少泄露，但是窗函数本身对频谱也会产生一定的影响。

平均

perter avitabile^[1]提到平均可以减少泄露。

 参考文献

[1] perter avitabile. modal testing: a parctitioner’s guide[m]. wiley. 2017